题目描述
如图:有n个重物,每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞,然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的(不会造成能量损失),桌子足够高(因而重物不会垂到地上),且忽略所有的摩擦。
问绳结X最终平衡于何处。
注意:桌面上的洞都比绳结X小得多,所以即使某个重物特别重,绳结X也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
输入输出格式
输入格式:
文件的第一行为一个正整数n(1≤n≤1000),表示重物和洞的数目。接下来的n行,每行是3个整数:Xi.Yi.Wi,分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )
输出格式:
你的程序必须输出两个浮点数(保留小数点后三位),分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。
输入输出样例
输入样例1:
1 | 3 |
输出样例1:
1 | 0.577 1.000 |
题解
一道物理题,也可以用模拟退火来瞎搞。正解要用到计算几何内容
先设平衡点为x,y,然后对所有的点产生的力正交分解,然后算合力。
但是也可以这样想:物重一定,绳子越短,重物越低,势能越小,势能又与物重成正比,所以,只要使得$\displaystyle \sum_{i=1}^n dis[i]\times weight[i]$也就是总的重力势能最小,就可以使系统平衡
这道题目的退火模型很典型,有些地方别的退火题目可能都用不到,模拟退火的细节看注释。
值得注意的是,$\displaystyle e^{-\frac{\Delta}{t}}$是一个退火公式,不一定是必须的,但是模拟退火里面用上它能更高效一点。
代码
1 |
|
补充
关于上面提到的退火公式有一个有趣的现象,当Δ>0时(具体来说是=5),我们的不是更优的,这个函数的图像是这样的(渐进1):
而当Δ=0时,函数恒为1
Δ<0时(具体来说是=-5),解更优,它的函数图像是这样的(渐进1):
Δ的变化动图: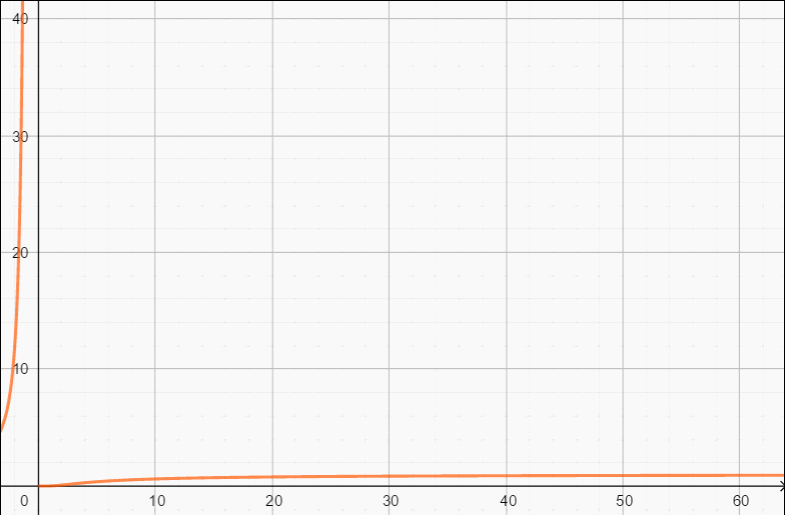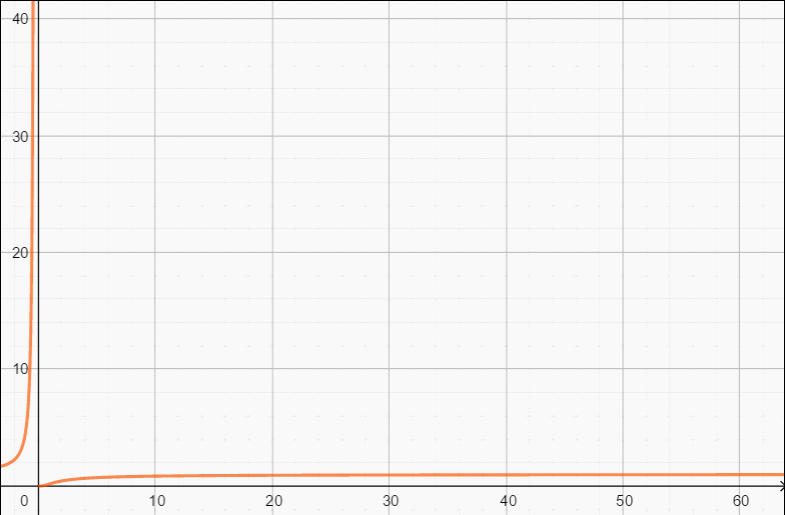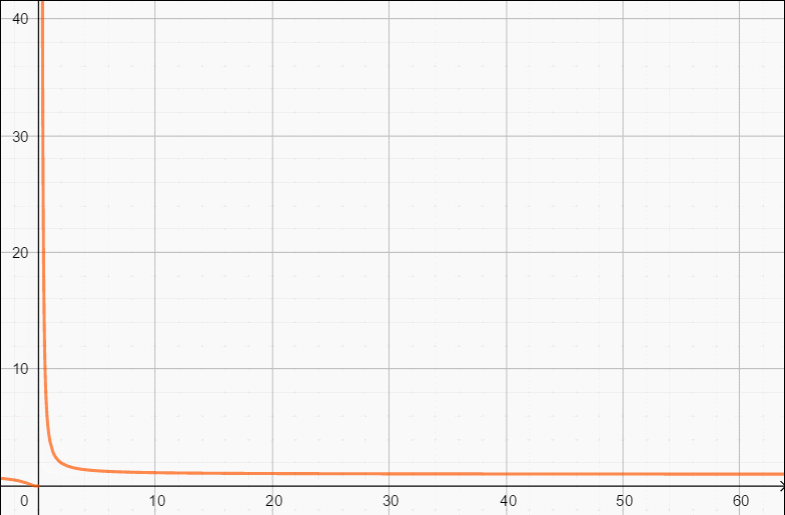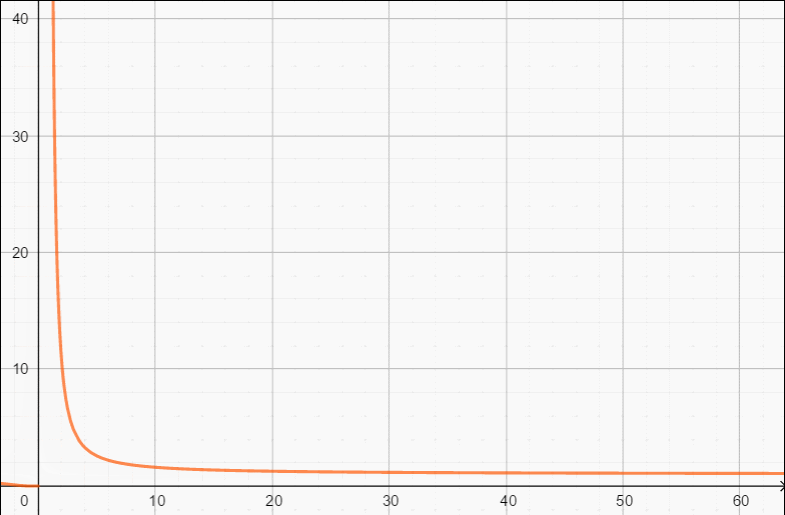
而1对于上面的程序是一个分界点,我们可以总结出规律来:
- 当解不是更优时,当温度越高时我们有更大的几率接受这个解,反之
- 当解是更优时,我们一定接受它